On the last few weeks I have been studying SAT/SMT solvers, how they work, but specially, how they relate to declarative programming. One of these problems that SAT claims to solve well is scheduling. Often, people claim to have another solution to a ultra-specialised Travelling Salesman Problem, only to be beat by converting to SAT/SMT, that also happily supports arbitrarily different clauses, thus being more flexible.
The problem
In order to try my understanding of SAT solving, I have recently worked on a small scheduling problem. The problem comes from Emmanuel Hebrard's slides for Scheduling and SAT. Here is the scheduling diagram:
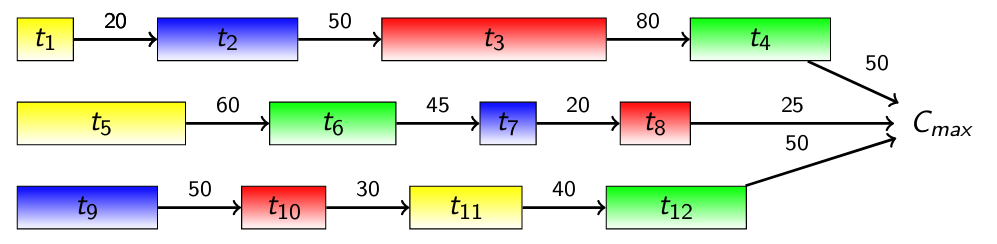
This is a small problem, but characterises quite a few details. We have three processes, made each one out of four steps. On each process you have to complete a step before you can start the next one. Finally, each step has a different colour, which identifies that the step cannot be run concurrently with another step of the same colour. We can imagine this arbitrary restriction as the step requiring a special machine, and we only have a single of each special machine in the workshop.
The question is: in what order do we execute the steps so that the total time is minimised? Let's work a solution with Z3 and Python.
The solution
First, let's do some setup and get some data of the times that take each step:
from z3 import *
task_length = {
1: 20,
2: 50,
3: 80,
4: 50,
5: 60,
6: 45,
7: 20,
8: 25,
9: 50,
10: 30,
11: 40,
12: 50
}
s = Optimise()Let's start defining a variable tX for the time for each step to start. All these times are greater or equal to zero.
tx = {k: Int("t{}".format(k)) for k in task_length.keys()}
s.add(And([t >= 0 for t in tx.values()]))All the processes will have finished at some time in the future, we will call it tend.
tend = Int("tend")Now for some restrictions: step 2 can't start before step 1 has finished, step 3 can't start before step 2 has finished, and so on. Also, tend cannot be smaller than the time when the last step has finished:
for i in [1, 2, 3]:
s.add(tx[i] + task_length[i] <= tx[i+1])
s.add(tx[4] + task_length[4] <= tend)
for i in [5, 6, 7]:
s.add(tx[i] + task_length[i] <= tx[i+1])
s.add(tx[8] + task_length[8] <= tend)
for i in [9, 10, 11]:
s.add(tx[i] + task_length[i] <= tx[i+1])
s.add(tx[12] + task_length[12] <= tend)Finally, the colouring restriction: steps 1, 5 and 11 can't run at the same time; the same for steps 2, 7 and 9; steps 3, 8 and 10; and steps 4, 6 and 12. To model this, the paper suggests adding a boolean variable for each pair: the boolean b1,5 will be true if step 1 goes before than step 5, otherwise it will be false. If it's true, we need a restriction that says that step 5 will start later than when step 1 has finished, otherwise step 1 will start later than when step 5 finishes. We don't know the value of these booleans, but the solver will fill them for us.
def add_related_constraint(s, a, b):
bo = Bool("b{},{}".format(a, b))
s.add(
If(bo, tx[a] + task_length[a] <= tx[b], tx[b] + task_length[b] <= tx[a]))
add_related_constraint(s, 1, 5)
add_related_constraint(s, 5, 11)
add_related_constraint(s, 1, 11)
add_related_constraint(s, 2, 7)
add_related_constraint(s, 7, 9)
add_related_constraint(s, 2, 9)
add_related_constraint(s, 3, 8)
add_related_constraint(s, 8, 10)
add_related_constraint(s, 3, 10)
add_related_constraint(s, 4, 6)
add_related_constraint(s, 6, 12)
add_related_constraint(s, 4, 12)And we are pretty much done! We make the solver do its stuff, and carefully format the output to be in the format we want to see:
s.minimize(tend)
print s.check()
m = s.model()
for i in sorted(task_length.keys()):
print tx[i], m[tx[i]]
print tend, m[tend]See the full code in Github.
The results are just nice:
sat
t1 0
t2 50
t3 100
t4 180
t5 20
t6 80
t7 125
t8 180
t9 0
t10 60
t11 90
t12 130
tend 230sat tells us that the solver has been able to satisfy all the restrictions, and then we have a list of all the task start times, and tend is 230. We know that we have to start first t1 and t9, then wait 20 before starting t5 and so on. Everything will be finished at 230. Very nice.
Further thoughts
SAT/SMT solving has been so far weird from my point of view. It strongly feels like a Prolog on steroids that can solve many problems without actually telling it how to do it. It thus touches quite a bit the "declarative" vibe for me. As you can see from the program before, I specified a bunch of restrictions and told Z3 to "go figure it out", and it did. In some sense, this is a kind of magical power. But programming didn't just dissappear. Now I need to figure out how to convert problems into the rightful SAT/SMT format, and this is a kind of programming in itself.
I will devote further exploring to SAT/SMT solvers in order to figure out more places where they are useful, as it seems to be a very interesting approach for some harder problems.